Unleash the Power of Data Compression: Explore Huffman Coding with Go

🎙️ Listen: Explore Huffman Coding

Ever wondered how your large files shrink to a fraction of their size when you zip them? Or how streaming services deliver high-quality video without constant buffering? Huffman coding stands as a fundamental hero behind much of this digital magic. It forms the cornerstone of lossless data compression, meaning it shrinks files without losing a single piece of original information.

Understanding how it works, with its frequency tables, binary trees, and variable-length codes, can sometimes feel like decoding a secret language itself. This post demystifies the core concepts of Huffman coding and shows you how Go (Golang) implements these principles.

Dive in and learn the secrets of efficient data storage and transmission!

1. What is Huffman Coding and Why Does It Matter?

At its heart, Huffman coding offers a brilliant strategy: assign shorter codes to frequently occurring characters (or bytes) and longer codes to less common ones. Think of it as a smart shortcut system. If you say “the” a hundred times a day, you’d want a very quick way to write it; meanwhile, a word you use once a year could have a longer, more unique symbol.

The Essence of Huffman: Variable-Length Codes

This “shortcut” approach leads to significant data compression. Importantly, unlike “lossy” compression (like JPEG images or MP3 audio, which discard some data), Huffman coding is lossless. This means you get an exact, byte-for-byte replica of the original when you decompress a Huffman-encoded file.

Why Huffman Matters: Real-World Impact

So, why is this so important?

• Efficient Storage: Smaller files take up less space on your hard drives, SSDs, and in cloud storage.
• Faster Transmission: Compressed data travels quicker across networks, improving download speeds and reducing bandwidth usage.
• Underpins Modern Tech: Formats like PKZIP, JPEG (for encoding parts of the data), and various network protocols widely use it.

Ready to see how this genius algorithm works?

3. The Core Principles Explained: From Frequencies to Codes

The magic of Huffman coding lies in three interconnected core principles:

Frequency Analysis: The Data’s Voice

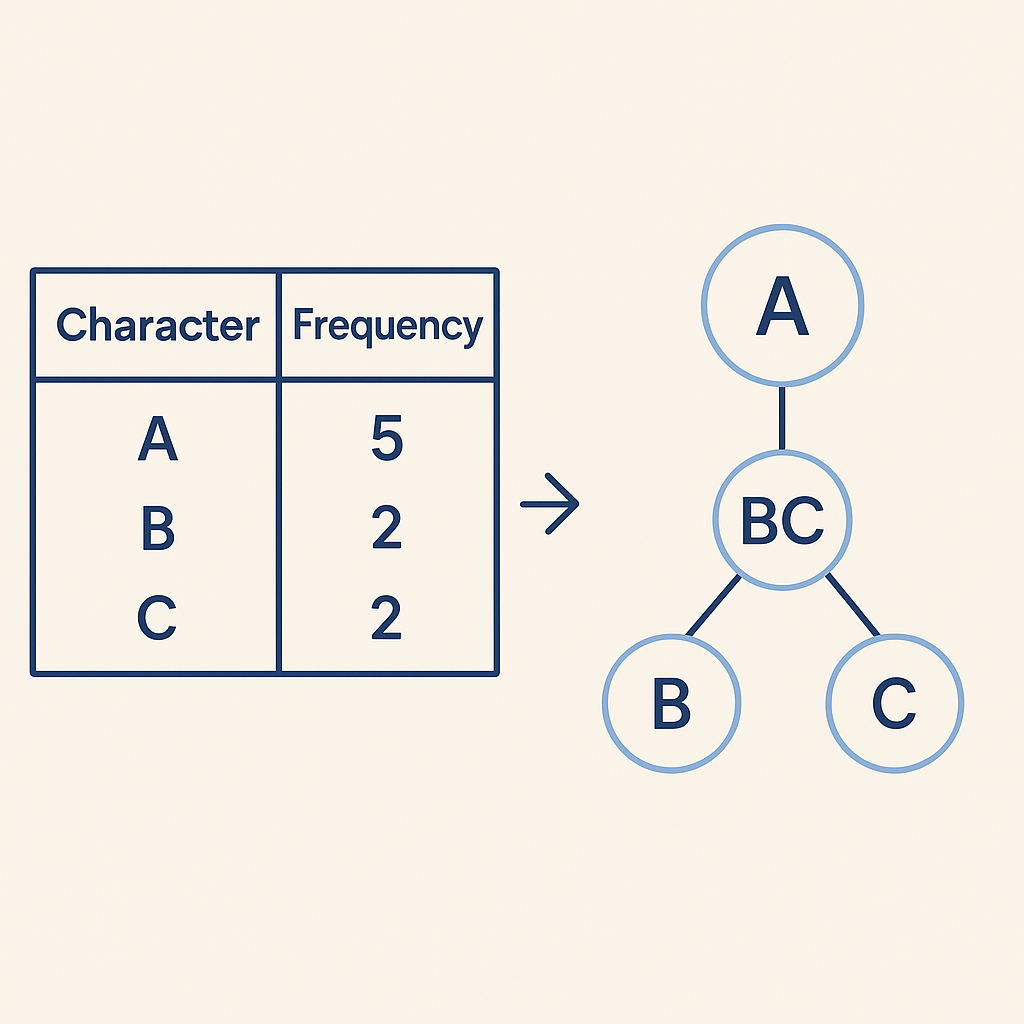
The journey begins by listening to your data. We count how many times each unique character (or byte) appears in the input. This “frequency map” then becomes the blueprint for compression. Characters that “speak” more often receive special treatment.

• Example: In “BCAAAACBC”, ‘A’ appears 5 times, ‘B’ twice, and ‘C’ twice. Clearly, ‘A’ is the most frequent!

The Huffman Tree: Building the Efficiency Map

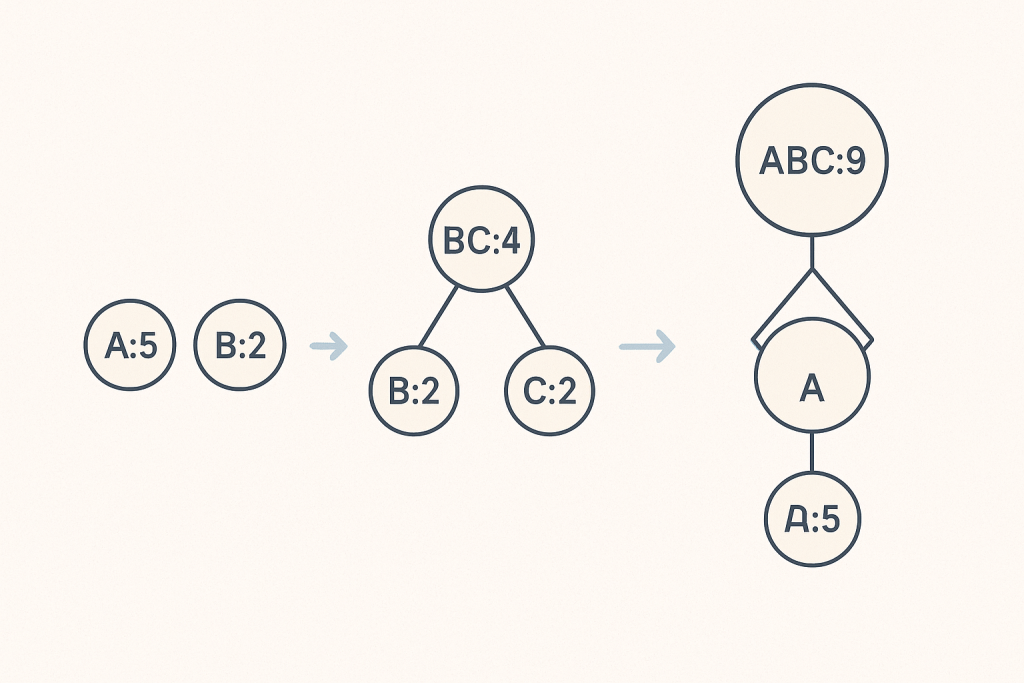
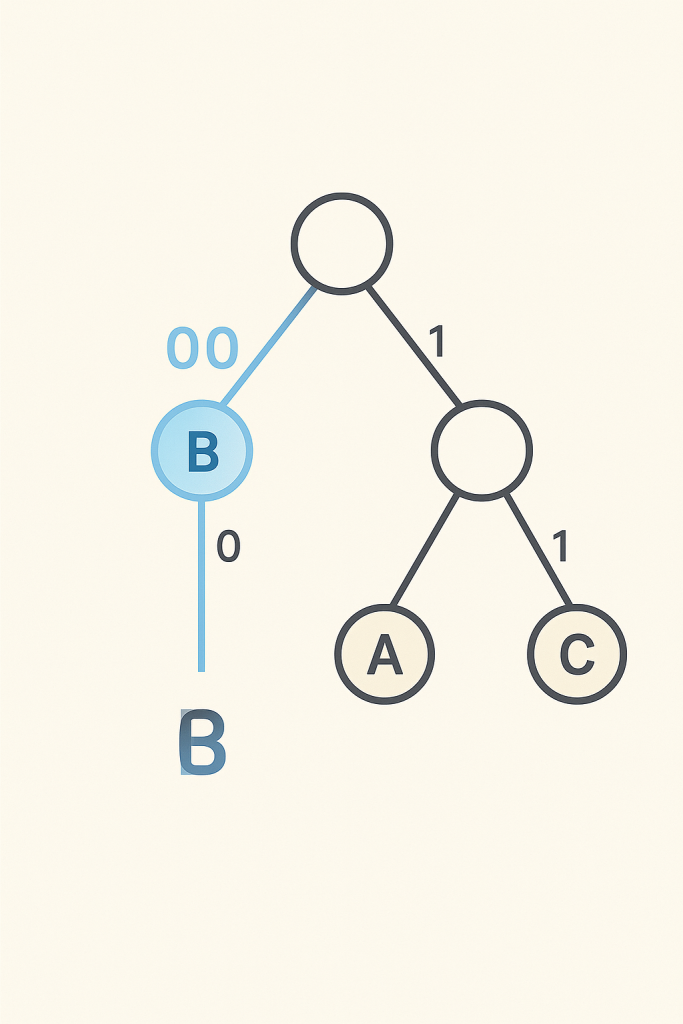
Using these frequencies, we construct a special binary tree (a “prefix tree”). The process involves several steps:

1. Start with each unique character as a “leaf” node, carrying its frequency.
2. Repeatedly pick the two nodes with the lowest frequencies.
3. Combine them into a new “parent” node whose frequency is the sum of its children’s.
4. Place this new parent back into the mix. This continues until only one node remains – the root of your Huffman tree. Consequently, the most frequent characters end up closer to the root, naturally leading to shorter paths.

Prefix-Free Codes: No Room for Confusion

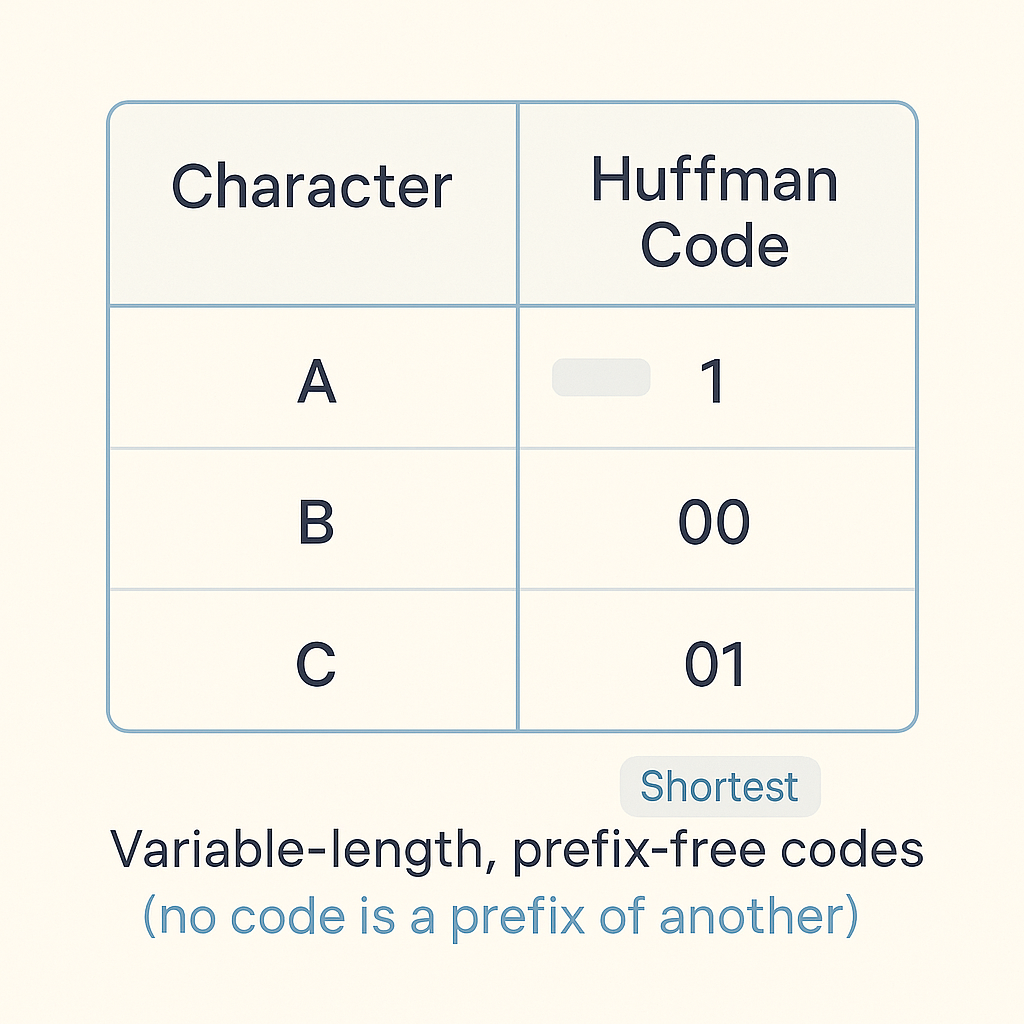
Once the tree builds, each character gets its unique binary code (a sequence of 0s and 1s) by tracing the path from the root to its leaf node. For instance, a left branch might be ‘0’ and a right branch ‘1’. The genius here lies in the fact that no character’s code is a prefix of another character’s code. This “prefix-free” property allows the decoder to read a stream of bits without needing separators, knowing exactly when one character’s code ends and the next begins. It’s truly brilliant!

3. Huffman Coding in Action: Implementing in Go

Understanding the theory is one thing; seeing it implemented in code truly brings the concepts to life. We now walk through the core components of a Huffman coding implementation using Go, a language known for its efficiency and strong standard library. While a full file compression utility involves robust file I/O and header management, we focus on the algorithmic heart.

3.1. Frequency Analysis in Go

The first step is to count character occurrences. In Go, we use a map[byte]int to store frequencies.

// Simplified function to build a frequency table from a string
func buildFrequencyTable(text string) map[byte]int {
    freqTable := make(map[byte]int)
    for i := 0; i < len(text); i++ {
        freqTable[text[i]]++
    }
    return freqTable
}

3.2. Building the Huffman Tree

The Huffman tree is constructed using a min-priority queue. Go’s container/heap package helps us manage this efficiently. We define a HuffmanNode struct and implement the heap.Interface for our PriorityQueue type, ensuring nodes are ordered by frequency.

// HuffmanNode represents a node in the Huffman tree.
type HuffmanNode struct {
    Char  byte         // The character (byte) this node represents (only for leaf nodes)
    Freq  int          // The frequency of the character or sum of children's frequencies
    Left  *HuffmanNode // Left child
    Right *HuffmanNode // Right child
}

// buildHuffmanTree constructs the Huffman tree from a frequency table.
func buildHuffmanTree(freqTable map[byte]int) *HuffmanNode {
    // PriorityQueue setup and heap operations (simplified for brevity)
    // The core logic repeatedly combines two lowest frequency nodes
    // until only the root remains.
    // Example:
    // pq := make(PriorityQueue, 0)
    // heap.Init(&pq)
    // for char, freq := range freqTable { heap.Push(&pq, &HuffmanNode{Char: char, Freq: freq}) }
    // for pq.Len() > 1 {
    //     left := heap.Pop(&pq).(*HuffmanNode)
    //     right := heap.Pop(&pq).(*HuffmanNode)
    //     parentNode := &HuffmanNode{Freq: left.Freq + right.Freq, Left: left, Right: right}
    //     heap.Push(&pq, parentNode)
    // }
    // return heap.Pop(&pq).(*HuffmanNode)
    return nil // Placeholder for actual root in full implementation
}

3.3. Generating Huffman Codes

Once the tree is built, we traverse it to assign binary codes. A recursive function is ideal for this, building the code as it moves down the tree.

// generateHuffmanCodes recursively generates Huffman codes.
func generateHuffmanCodes(node *HuffmanNode, currentCode string, codes map[byte]string) {
    if node == nil {
        return
    }
    if node.Left == nil && node.Right == nil { // This is a leaf node (character)
        codes[node.Char] = currentCode
        return
    }
    generateHuffmanCodes(node.Left, currentCode+"0", codes)  // Go left, append '0'
    generateHuffmanCodes(node.Right, currentCode+"1", codes) // Go right, append '1'
}

3.4. Encoding Data

Encoding involves replacing each original character with its Huffman code. These binary codes are then packed efficiently into bytes for storage, as files are stored as sequences of bytes, not individual bits.

// Simplified encoding loop snippet (illustrates bit concatenation)
func encodeData(text string, codes map[byte]string) string {
    var encodedBits string
    for i := 0; i < len(text); i++ {
        encodedBits += codes[text[i]]
    }
    // In a real file compression, these bits would be packed into bytes
    // and written to a file, along with padding information.
    return encodedBits // Returns a string of '0's and '1's for illustration
}

3.5. Decoding Data

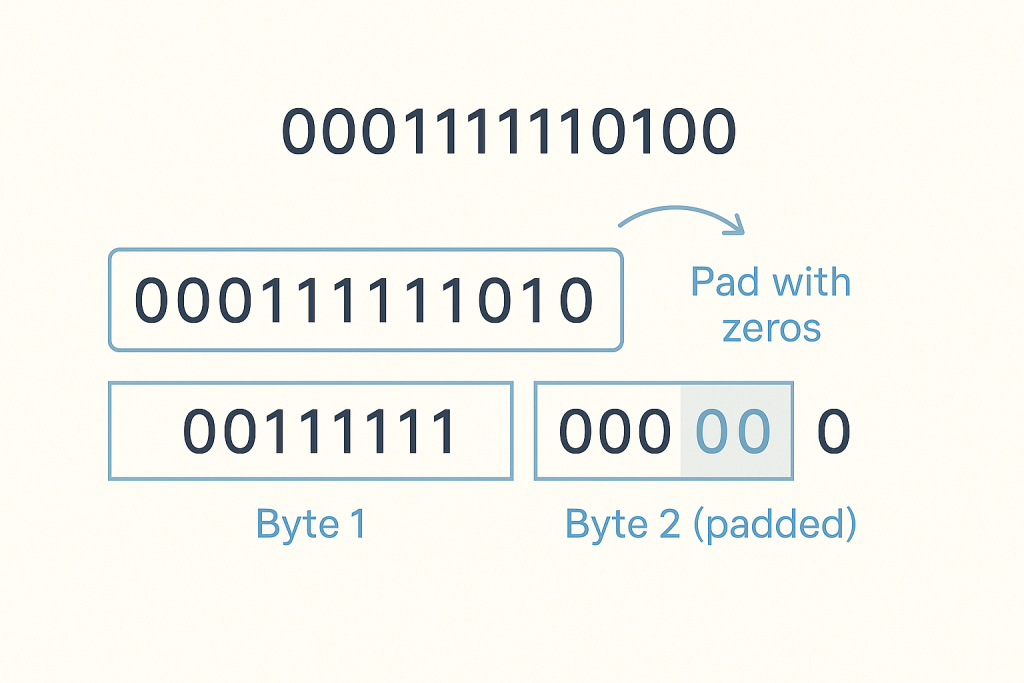
Decoding reverses the process. We read the bitstream, bit by bit, and traverse the Huffman tree. When a leaf node is reached, the character at that node is the original character, and we reset to the root of the tree to decode the next character.

// Simplified decoding loop snippet (illustrates tree traversal)
func decodeData(encodedBits string, root *HuffmanNode) string {
    var decodedText string
    currentNode := root
    for _, bit := range encodedBits {
        if bit == '0' {
            currentNode = currentNode.Left
        } else { // bit == '1'
            currentNode = currentNode.Right
        }
        if currentNode.Left == nil && currentNode.Right == nil { // Reached a leaf node
            decodedText += string(currentNode.Char)
            currentNode = root // Reset to root for the next character
        }
    }
    return decodedText
}

Conclusion: Empowering Your Data Journey

Huffman coding is more than just an algorithm; it’s a testament to how clever mathematical approaches can solve real-world problems like efficient data management. By exploring its core principles and seeing how they translate into Go code, you’ve gained a deeper understanding of lossless data compression.

We hope this guide empowers you to not only grasp complex technical concepts but also to enhance your own web presence with valuable, informative content.

For complete code visit : Go PlayGround

Happy compressing (and decompressing)!