Algorithms at Altitude: The Secret Sauce Behind Sindoor’s Precision Hits

Early on May 7 2025, India executed Operation Sindoor—a series of precision missile strikes on nine terrorist facilities inside Pakistan and Pakistan‑Occupied Kashmir. The objective: dismantle the infrastructure used by groups such as Lashkar‑e‑Taiba (LeT), Jaish‑e‑Mohammed (JeM) and Hizbul Mujahideen (HM) without harming surrounding civilian areas. Over a 26‑minute window (01:04–01:30 IST) 24 guided munitions found their marks.

While headlines centred on the political stakes and the hardware—SCALP cruise missiles, HAMMER precision bombs, and loitering munitions—the real star was the math running silently inside every seeker head. This post peels back the shroud on those algorithms and shows why they matter.

🎙️ Listen:The Secret Sauce Behind Sindoor’s Precision Hits

Why Guidance Algorithms Matter

1. Civilian Safety – The closer a weapon can stay to its optimal flight path, the smaller the lethal radius required, dramatically reducing collateral damage.
2. Strategic Signalling – Surgical accuracy signals technological superiority while containing escalation.
3. Cost Efficiency – Fewer weapons expended for the same effect lowers mission cost and logistical footprint.
4. Multi‑Domain Coordination – When Navy, Air‑Force and Army assets share one battlespace, algorithmic predictability prevents fratricide and simplifies command‑and‑control.

Behind the Seeker: Proportional Navigation (Pro‑Nav)

One of the oldest—and still most effective—homing strategies is Proportional Navigation (PN).
Core idea: if the missile keeps the rotation rate of its velocity vector proportional to the rotation rate of the line‑of‑sight (LOS) to the target, the two paths converge.

The normal acceleration required is

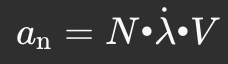
where:

• N – navigation constant (typically 3–5)
• LOS – angular rate (rad/s)
• V – closing velocity (m/s)

If LOS spikes because the target jinks sideways, the missile instantly commands a larger turn. If the LOS is steady, only small corrections are needed.

Augmented PN and modern Kalman‑filter variants layer in target acceleration, 3‑D gravity compensation, and multi‑sensor fusion—but the PN backbone remains recognisable.

Algorithms at Work in Operation Sindoor

• SCALP/Storm Shadow cruise missiles used a TERCOM‑enhanced variant of PN for the terminal dive, integrating terrain contour maps and an imaging‑infra‑red seeker to achieve sub‑metre Circular Error Probable (CEP).
• HAMMER smart bombs rode differential‑GPS cues during mid‑course, then switched to laser‑spot PN homing when the designator illuminated the target.
• Loitering munitions (“kamikaze drones”) employed image‑based scene‑matching plus a PN‑derived course law once the onboard vision system recognised the aim‑point.

The synergy of these systems enabled Indian planners to strike specific buildings within dense urban clusters such as Muridke and Bahawalpur, while leaving adjacent civilian structures intact.

Interactive Demo

Try adjusting missile speed, selecting targets, and pressing L to launch—the proportional-navigation logic guides each missile to its mark.

Website: https://sindoor.oofn.in/

Quick Python Taste of PN

"""A *very* simplified 2‑D proportional‑navigation interceptor demo."""
import numpy as np

def proportional_navigation(target_pos, missile_pos, missile_vel, N=4, dt=0.05, hit_radius=1.0, steps=2000):
    traj = []
    for _ in range(steps):
        rel = target_pos - missile_pos
        dist = np.linalg.norm(rel)
        if dist <= hit_radius:
            break  # target hit
        # LOS unit vector and its rate (finite difference approximation)
        losu = rel / dist
        # angular rate approximation
        vel_cross = np.cross(np.append(missile_vel, 0), np.append(losu, 0))
        lam_dot = vel_cross[2] / (dist ** 2)
        # command normal acceleration (perpendicular to velocity)
        accel = N * lam_dot * np.linalg.norm(missile_vel)
        # rotate acceleration into the plane
        normal = np.array([-missile_vel[1], missile_vel[0]])
        normal /= np.linalg.norm(normal)
        missile_vel += accel * normal * dt
        missile_pos += missile_vel * dt
        traj.append(missile_pos.copy())
    return np.array(traj)

Run the function with initial positions and plot the trajectory to see how the missile curves onto the target.

Conclusion

Operations like Sindoor remind us that the cutting edge of national defence lies as much in lines of code as in tonnes of steel. Precision isn’t an adjective; it’s an algorithm. The next time global headlines speak of “surgical strikes,” remember the invisible mathematics guiding each weapon from launch to impact.